PFC models for vapour-liquid-solid coexistence and transitions

Kocher et al. [1] included the vapour model into the standard PFC framework, and arrived at the following model:

where \(n_{mf}(\mathbf{r})=\int d\mathbf{r}' \chi(\mathbf{r}-\mathbf{r}')n(\mathbf{r}')\) is defined as the "density mean-field". The bulk compressibility and the strength of the anisotropy in the periodic phase is controlled by $B^x$, while \(B^\ell\) corresponds to the inverse compressibility of the liquid phase, such that \(\Delta B=B^\ell-B^x\) acts as an effective temperature parameter. This model considers the original two-point correlation function proposed by Elder et al., i.e. \(\hat{C}_2(\mathbf{q})=1-\Delta B -B^x(|\mathbf{q}|^2-1)^2\), in Fourier space, which produces triangular (BCC) solid phase in 2D (3D). The terms coupling the density to its mean-field result from incorporating higher-order correlations, which are defined as smoothing kernels designed to operate only on the long wavelength of the density field as \(\hat{\chi}(\mathbf{q})=\exp[-|\mathbf{q}|^2/2\lambda^2]\). This approach was the starting point of this class of vapor PFC models that consider effective higher-order correlations to control the liquid and vapor phases.

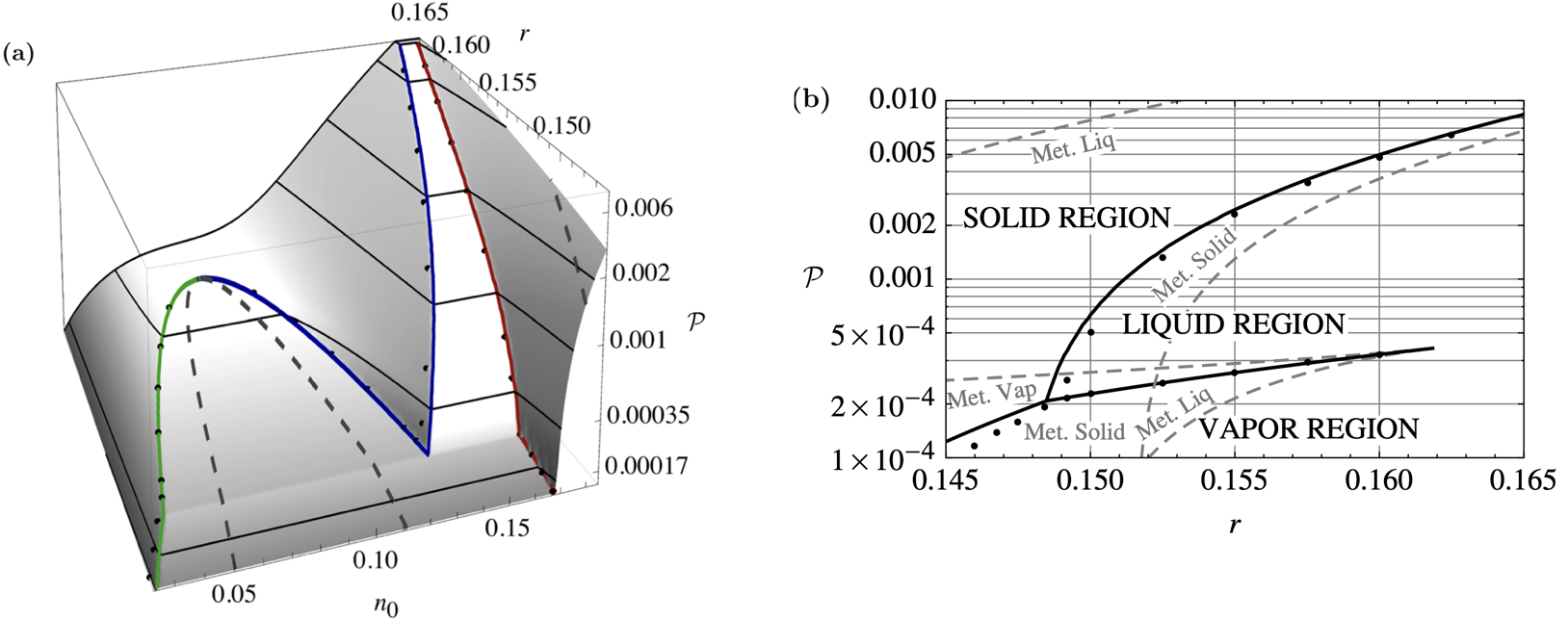
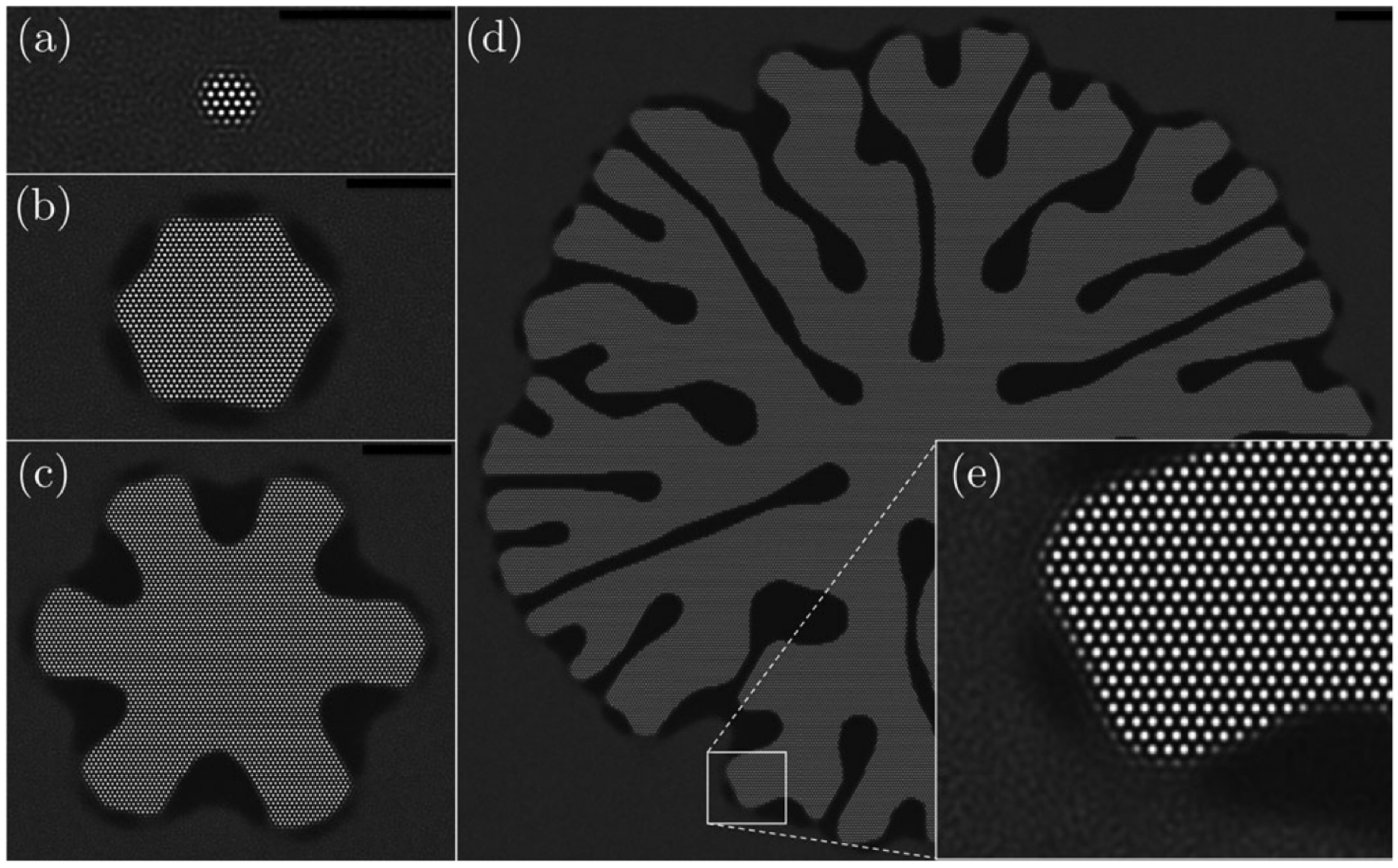
Jreidini et al. considered a more generalized version of Kocher's model, in which all parameters are temperature dependent (up to second order), and now the two-point direct correlation is designed as in XPFC models, with Gaussian peaks.

This new formalism introduced here allows for novel, and experimentally relevant, applications in solid-vapor growth to be explored. Our theory captures the thermodynamics of pure substances excellently, while maintaining a funda- mental connection with all elastoplastic properties of solids. The formalism introduced here offers new tools to model experimental processes in the fields of crystal growth (chemical vapor deposition or vapor-solid-liquid growth) or soft matter systems (phase separation in polymers, polymer crystals, or colloidal suspensions).