Pattern formation in the Bénard-Marangoni convection
Numerical results obtained for the equation derived by E. Knobloch used to study long wavelength pattern formation in the Bénard-Marangoni convection:
\[ \dfrac{\partial u}{\partial t}=\alpha u-\mu \nabla^2u-\nabla^4u+ \nabla \cdot \bigg[ k|\nabla u|^2\nabla u+ \beta\left(\nabla^2 u \nabla u \right) - \gamma u \nabla u + \delta \nabla|\nabla u|^2 \bigg] \nonumber \] Generalized Dirichlet boundary conditions (\(u={\partial u}/{\partial n}=0\)) are assumed for the numerical integration of the governing equation. The numerical scheme consisted of the classical operator splitting scheme of stabilizing correction [4], presenting fourth-order diffusion operators. The \(L_1\) norm was used to measure the rate of change of the distance between two successive states of the system, therefore, it is sensitive to the evolution of both the amplitude and the phase. Steady states assumed for \(L_1 \leq 1 \times 10^{-6}\).
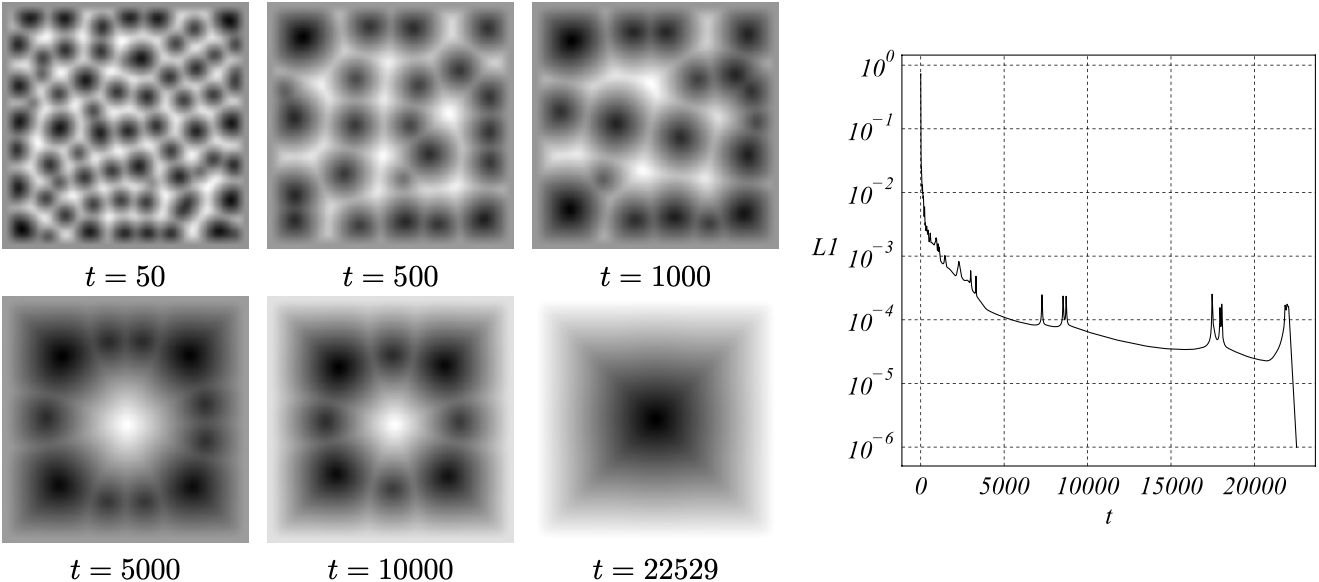
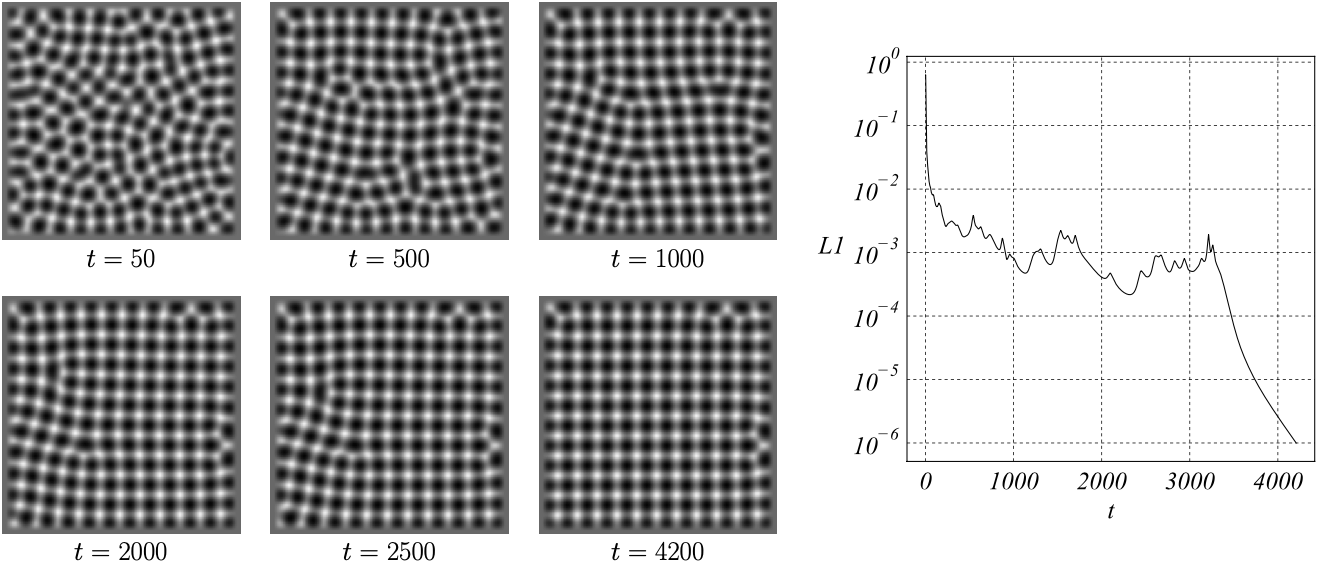
FIG. 1 shows results obtained for: \(\alpha=0.0\), \(\mu=2.0\), \(k=1\), \(\beta=-0.125\sqrt{7}\), \(\gamma=0.0\) and \(\delta=0.75\sqrt{7}\). FIG. 2 shows results obtained for: \(\alpha=-0.8\), \(\mu=2.7\), \(k=1\), \(\beta=-0.125\sqrt{7}\), \(\gamma=0.0\) and \(\delta=-0.75\sqrt{7}\). The grid is uniform, structured and staggered with a resolution of \(8\) points per wavelength. This corresponds to a square domain of \(10 \times 10\) wavelengths per side length.
References
[1] L. Shtilman, and G. Sivashinsky, Physica D, 52(2-3), 477-488 (1991).[2] M. Bestehorn, Physical Review E, 48(5), 3622 (1993).
[3] C.I. Christov, J. Pontes, D. Walgraef, and M.G. Velarde, CMAME, 148(3-4), 209-224 (1997).
[4] Yanenko, N. N., The Method of Fractional Steps, New York: Springer, (1971).
